Nutritional scientists break down energy consumption into three components. The largest is Resting Energy Expenditure (REE), which I’ve examined in detail in the previous post. It accounts for 60-80% of our daily energy consumption. REE is the energy consumed at rest, when there’s no physical activity going on. Another 5-10% is used for digestion. The rest of our energy consumption is due to physical activity. These proportions can vary: if you’re a rider in the Tour de France, your daily physical activity will probably exceed your REE several times over.

The workout

Energy consumption by the body in motion is illustrated by what happens when we go to the gym, which is always a good thing to do. We might step onto an elliptical cross trainer, where the arms, as well as the legs, provide power. A well-equipped machine registers how many Calories are expended per hour, and also the work output — how much power is being delivered to the pedals and the levers.

Let’s look at those numbers for a 74-kilogram (165 pound), 35-year-old man, height 178 cm (5 feet 10 inches). Let’s say our gym guy is reasonably fit. Once he gets warmed up on the elliptical, the readout indicates that he is burning 800 Calories an hour. That’s fairly strenuous exercise, which he continues for half an hour. The resulting energy burn, 400 Calories, makes up a significant part of his daily energy use, which for him would be around 2,500 Calories (estimated using a web site maintained by the Mayo Clinic).

Looking at another measure of the workout, he might see that he’s delivering power to the machine at a rate of 195 watts, a level he knows from reading cycling magazines is pretty good for him. This number is the work output. (A rider in the Tour de France would put out an average of near 300 watts for several hours, and peak at higher levels.)

What’s the relationship of the watts being delivered to the machine to the calories being consumed by the body? The total energy consumed in a physical activity, whether it’s walking 10 kilometers or lying in bed, is usually measured in Calories, with a capital C, which is equal to 1,000 of the scientist’s small-c calories. Packaged food comes with its energy content expressed in Calories, and our daily energy needs are usually expressed in Calories.

Our man at the gym is burning energy at a rate of 800 Calories an hour. His work output, the rate that power is being delivered to the pedals, is 195 watts. Power is a measure of how fast we’re using or producing energy; the big element on top of an electric stove may put out 1,000 watts of power on the medium setting. It would consume 1,000 watt-hours of energy in an hour, or as we usually call it, a kilowatt hour (abbreviated kWh). The electrical utility company bills us according to how many kWh we consume in a month.

The Calorie, and the kWh, are both measures of the amount of energy consumed or produced. The conversion is simple: 1,000 Calories is 1.162 kWh. The 195 watts of work output delivered to the exercise machine by our man in the gym equals 168 Calories per hour. That’s only 21% of the total of 800 Calories per hour consumed by his body. What’s going on?

The distribution of energy use for our man pumping the elliptical cross trainer, and at rest, is shown graphically in Figure 1.

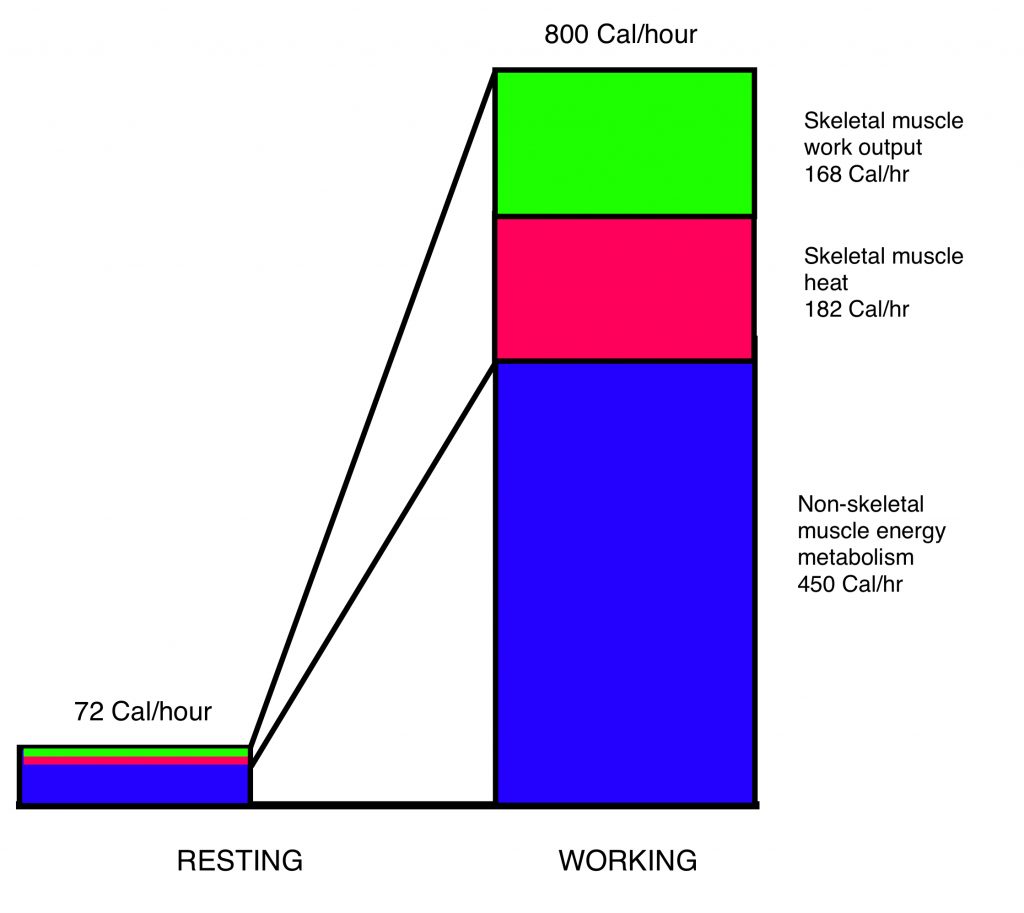
Part of the difference between the total Calories expended, and the Calories of actual work performed, is due to the efficiency of energy metabolism. About 54% of the energy potentially available in the carbohydrates, fat, and protein of food is converted to the bond energy of ATP, the common currency of energy metabolism. There are other, smaller, losses in the muscle itself, such as the friction between actin and myosin filaments sliding over each other. Direct measurements show that the overall efficiency of muscle work during aerobic exercise is about 48% (1). The rest goes to heat. So the total energy requirement for the 168 Calories per hour of work output would be 168/.48, or 350 Calories per hour. Of this, 182 Calories per hour (350-168) ends up as heat.

The total energy consumption of the working muscles, 350 Calories per hour, is still much less than the 800 Calories per hour of energy consumed during the workout. The difference of 450 Calories per hour is due to the needs of all the other parts of the body. The brain and the adipose tissue don’t change much, but the systems needed to service intense exercise are called on to increase their work. The lungs, part of the “residual” organ system in the previous post, puff harder and more frequently than before. The heart may be beating three times faster than at rest. Most of the energy being consumed by the body of the man in the gym is not powering the contractions of his skeletal muscles.

Metabolic efficiencies

The ratio of work output, 168 Calories per hour in this case, to total energy metabolism, 800 Calories per hour, is the Gross Metabolic Efficiency, GME, which is 168/800, or 21%. The GME for most healthy, fit, people during vigorous exercise is between 15 and 25%, depending on the activity and their fitness — while measurements of bicycle riding are usually in the range 21-24%, while ski-racing, using the “skating” technique, was reported to be 15% for world-class athletes (2).

Some kinesiologists think that activities requiring complex technique, as skate-skiing does, may show a lower GME, compared to activities in which the activity is quite simple, like bicycle racing. However, technique and technology almost always affect GME; for example, both the cadence and pedal width of a stationary bicycle influenced GME (3, 4).  In that activity, as in others, the total energy consumed was proportional to the work output, resulting in a fairly constant GME. This is called the “Fenn effect”; it was discovered in the study of isolated frog muscles in 1923, but has subsequently been found to apply to human athletes as well (5).

Measuring the work output on a training machine is fairly straightforward. Stationary machines, or even bicycles in the field, can be equipped with force-sensitive outputs, and the watts produced can be measured directly. But measuring total fuel consumption is a bit of a science project. What needs to be determined is the rate at which carbohydrate, fat, and protein are being oxidized to CO₂. The most reliable method for doing this is indirect calorimetry, in which the subject wears a mask that measures the rate of oxygen taken in and CO₂ expelled. The calories consumed can then be calculated from the ratios of CO₂/ O₂, the “Respiratory Quotient”, which is known for different foodstuffs.

Indirect calorimetry is not amenable to the athletic field, especially if a high level of performance is important. There are other methods for determining total energy expenditure. The most accurate method is the “Doubly Labeled Water” (DLW) technique, which is innocuous and imposes no restrictions on the athlete in the field. Before the event, the athlete drinks water which is doped with the “heavy” stable isotopes of hydrogen (deuterium, H²) and oxygen (O¹⁸). Over time, the heavy water is equilibrated in the body’s tissue and molecules, Because all of the hydrogen is excreted in the urine, but oxygen is excreted both in urine and expired air, the difference between the isotopes in the urine can be used to determine the “missing” carbon, and thus the carbon dioxide expired. (Information about the ratio of different foods in the diet is also required.) This unobtrusive, but expensive method (expensive because of the cost of isotopes) was used to determine the total energy consumption of a group of Tour de France riders, and led to an estimate of 24% for their Gross Metabolic Efficiency.

GME is the ratio between work output and total metabolic activity (i.e., energy consumed). There are other ways of expressing efficiency, which are illustrated by a study of rowing machine efficiency (6). The GME for a group of 5 university oarsmen was 17.5%. When the baseline (resting) metabolism, the REE, was subtracted from the total metabolic energy (which is reasonable, since it doesn’t contribute to the work output), the “net efficiency” was 19.8%.

In Figure 1, the net efficiency would be 168/(800-72), or 23%, compared to 21% for GME. A third method is to compare the graph of work output vs energy metabolism. For the rowing machine study that yielded a value of 22.8%. This is the “work efficiency”; the slope is very close to a straight line, because energy metabolism is proportional to work (the Fenn effect). And subtracting the metabolism required for the motions of rowing with no “load” as a baseline resulted in a “delta efficiency” of 27.5%. Kinesiologists use different analyses to compare changes in technique, training methods, equipment and other aspects of high-level performance. Even details such as the width of the pedal on a bicycle can influence efficiency (3)!

On July 14, 2016, Bastille Day, Thomas de Gendt of Belgium, won the twelfth stage of The Tour. This was the hardest day; it included almost 2,500-meters (8,500 feet) of climbing on Mount Ventoux to the finish line. De Gendt’s bike had special pedals and a hub that indicated his average power output for the ride that day was 289 watts. Using the value 24% for GME, as previously determined for Tour riders, his total caloric consumption was just over 5,300 Calories for the 5 hours and 8 minutes it took him to reach the finish line of that day’s stage. Together with the energy he needed to get through the rest of his day, he needed to eat nearly 8,000 Calories worth of food to stay in energy balance.

Meanwhile, back at the gym, our man may wonder: “How did the elliptical machine determine that I was burning 800 Calories per hour?” Well, it didn’t. As explained above, determining the total metabolic energy output requires either indirect calorimetry or the doubly labeled water technique, neither of which is generally available at our local Y. But Gross Metabolic Efficiencies are fairly well known for different kinds of activities. The elliptical cross trainer was programmed at the factory to use the work output, which it measures directly (the input work drives a rotor against a resistance, and provides a direct readout of the power), and dividing it by the predicted GME. And that produces the value of Calories/hour you see on the machine’s digital readout. It’s a calculated number.

I thought I’d see what my own gym machine uses for that factor. So I worked out on the elliptical cross trainer at various rates, and also told the machine my weight (I lied about the weight in some cases, to see what effect it would have). The apparent GME values the machine used to convert my work output (watts) to Calories consumed per hour ranged between 16 and 23%, with lower values coming up with a high apparent body weight (big people need more energy just to drive the basic functions, so their apparent efficiency is lower) and the highest value for what was, for me, a high level of power (300 watts for about a minute; I’m not sure that was an accurate measure, but that’s what the machine’s readout said).

The company that made the elliptical trainer used a variable GME to convert work output to calories consumed per hour. But the idea that GME varies for a given activity may not always apply. On one hand, cyclists with different performance capacities (as reflected by their maximum oxygen intake per kilogram of body weight) had about the same GMEs, around 18-19%, and those values didn’t change much with intensity of effort (7). On the other hand, in another study, the measured GME decreased significantly when the cadence (pedal rate) was increased, at constant work load, on stationary bicycles (4). This indicates that technique, and technology, are important in establishing the metabolic efficiency. This was further supported by the finding that an activity that requires a high level of technical skill, cross-country skiing using the skating technique, showed a significant difference in GME between world-class racers on the one hand, and fit, but lesser, athletes on the other (2). But again, the degree of effort (work output rate) didn’t change the GME values for the two kinds of athletes. They simply had different GMEs, probably a result of their level of fitness and possibly genetics.

High performance

Bicycle racers are some of the fittest athletes in the world. Riders in the peloton can produce 800 watts of power for 15 seconds, and 600 for one minute. The strongest cyclists can put out 1200 watts of work for 15 seconds. A recreational rider weighing 70 kg (just over 154 lbs.) might be able to maintain a power output of 164 watts for 20 minutes, while the professional rider might produce 300 watts, or more. These twenty minutes at close-to-maximum effort would tire the recreational bicycle rider. The professional from the peloton would shrug off the effort and keep going. But as is clear in the analyses of performance described earlier, the main reason for the difference is probably not that the professional rider has a much higher Gross Metabolic Efficiency; rather, he or she can take in, and distribute to the tissues, a greater amount of oxygen per minute per kilogram of body weight than the recreational rider.

Eddy Merckx is considered by many to be the greatest cyclist who ever lived. He used to annihilate his opponents; his nicknames included “The cannibal” and “One man forest fire”. Although he didn’t eschew pharmaceuticals (he tested positive on several occasions, as did his competitors), it was universally agreed that he was the strongest rider in the world. One day in 1975, Merckx was put on a stationary bicycle and encouraged to go as hard as he could. He produced 455 watts of power for one hour, about twice what a fit young amateur rider can do. He had to have fans (electric, not human) blowing air over him to keep from overheating — he was probably generating about 1,900 watts, or 1,600 Calories per hour, of heat. You could sear a steak.

There is a limit to how much energy the human body will produce. Each year since 2015, a small group of extreme athletes undertakes to run across the United States, from Los Angeles to Washington, DC. Their energy output has been measured. Although during the initial phase there’s a high rate of energy consumption, after about 20 days the expenditure levels off at about 2.5 times the normal value (8). Shorter endurance races, like a marathon, can see higher levels, but over time, the human body adapts and conserves its energy stores.

Serious athletes are interested in the work rate, the ability to push their bodies to the maximum speed and strength. During training, they and their coaches bend every effort to increase their work rate, or power. For sports like bicycle racing or rowing, the best measure of performance is the power developed per kilogram of body weight. If a woman cyclist weighing 61 kilograms (134 pounds), and an 80-kilogram (176 pound) male cyclist can put out the same average rate of work, the woman will win a race between them; her work rate per kilogram is significantly higher.

The average recreational bike rider can expect to put out around 2 watts/kilogram of body weight. A professional racer in the Tour de France may develop more than 6. Each of them can go higher for brief periods, but there will always be a big difference between them. But as became clear in the analyses of performance described above, the basis of difference is most often not that the professional rider has a much higher Gross Metabolic Efficiency; rather, he can take in, and distribute to the tissues, a far greater amount of oxygen per minute.

Go to Latest Posts

Work cited

1. Barclay, C. J., R. C. Woledge, and N. A. Curtin. 2010. Is the efficiency of mammalian (mouse) skeletal muscle temperature dependent? The Journal of physiology 588:3819-3831.
2. Sandbakk, O., H. C. Holmberg, S. Leirdal, and G. Ettema. 2010. Metabolic rate and gross efficiency at high work rates in world class and national level sprint skiers. European journal of applied physiology 109:473-481.
3. Disley, B. X., and F. X. Li. 2014. The effect of Q factor on gross mechanical efficiency and muscular activation in cycling. Scandinavian journal of medicine & science in sports 24:117-121.
4. Leirdal, S., and G. Ettema. 2011. The relationship between cadence, pedalling technique and gross efficiency in cycling. European journal of applied physiology 111:2885-2893.
5. Brandt, P. W., and M. Orentlicher. 1972. Muscle energetics and the Fenn effect. Biophysical journal 12:512-527.
6. Fukunaga, T., A. Matsuo, K. Yamamoto, and T. Asami. 1986. Mechanical efficiency in rowing. Eur J Appl Physiol Occup Physiol 55:471-475.
7. Moseley, L., J. Achten, J. C. Martin, and A. E. Jeukendrup. 2004. No differences in cycling efficiency between world-class and recreational cyclists. International journal of sports medicine 25:374-379.
8. Thurber, C., L. R. Dugas, C. Ocobock, B. Carlson, J. R. Speakman, and H. Pontzer. 2019. Extreme events reveal an alimentary limit on sustained maximal human energy expenditure. Science advances 5:eaaw0341.